C1. Introduction : fonction diélectrique des métaux massifs et des nanoparticules métalliques
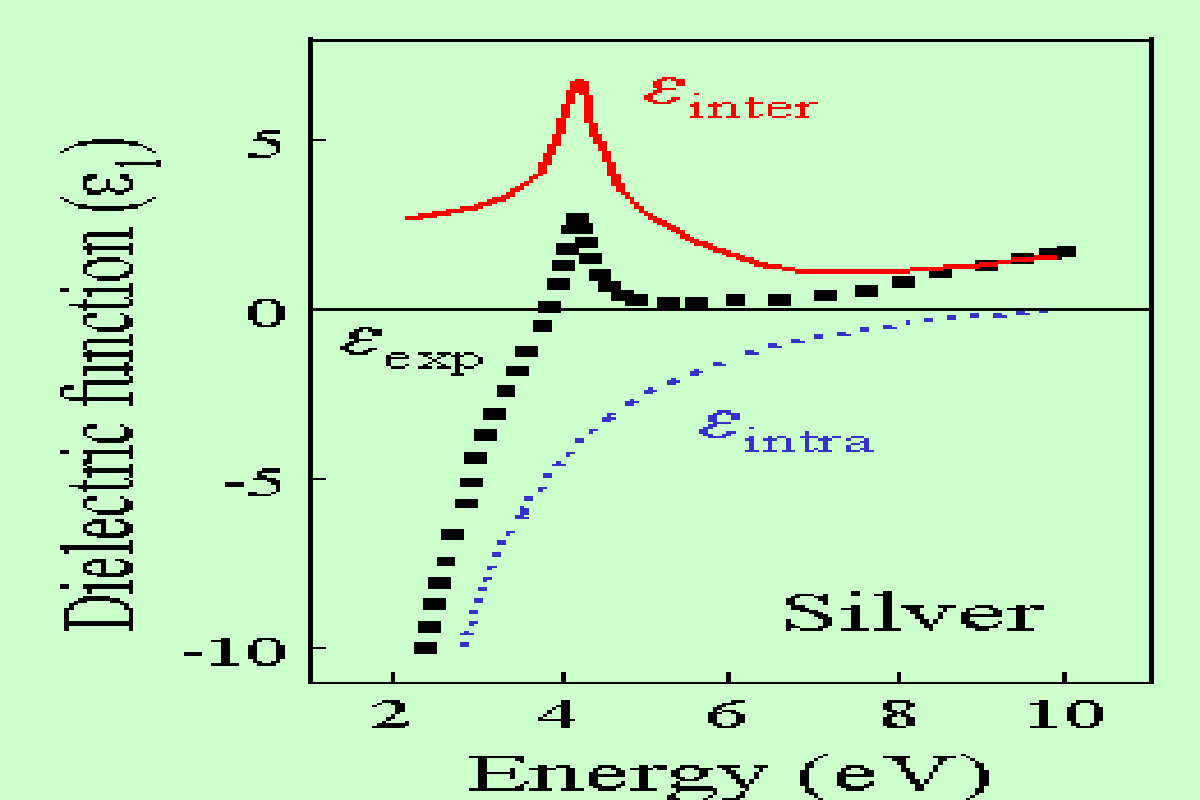
La réponse optique des métaux est dominée par deux contributions des électrons à la fonction diélectrique ε(q,ω) = εD(q,ω) + εib(q,ω). εD correspond aux électrons de conduction. Elle est associée aux processus optiques intrabandes (électrons et trous appartenant à la même bande) qui peuvent être décrit en première approximation par une fonction diélectrique de Drude. εib correspond aux processus optiques interbandes qui peuvent être décrit par la fonction diélectrique de Lindhard.
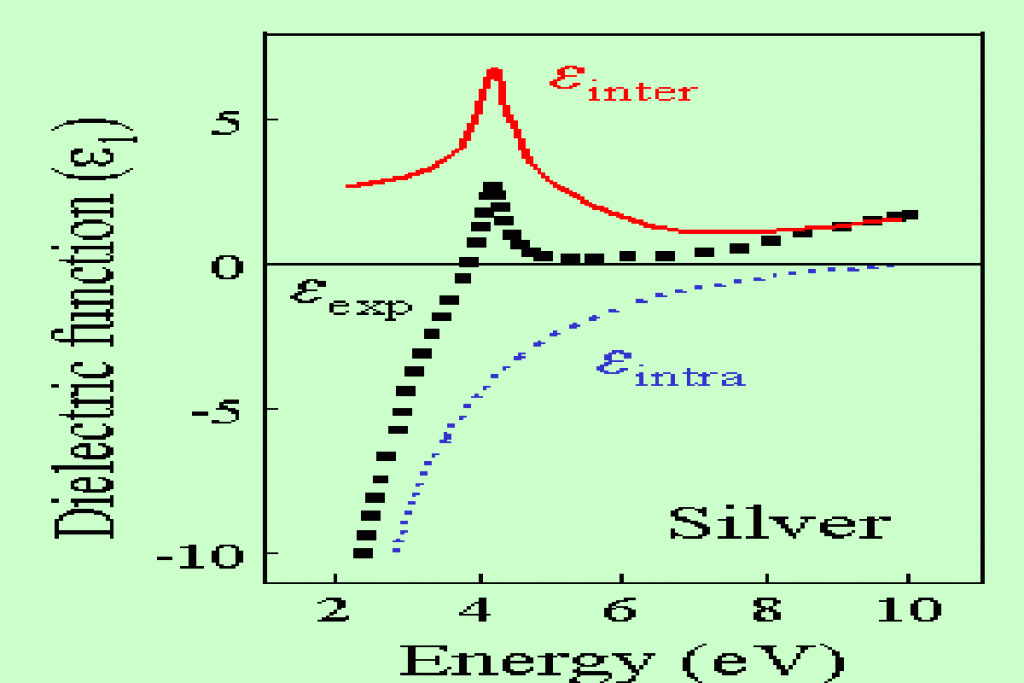
Figure 1 : Fonction diélectrique de l’argent.
|k,l>
électron de vecteur d’onde k dans la bande l ; f distribution de Fermi
Dirac ; hω énergie des photons. La figure 1 montre un exemple des
contributions intrabande et interbande à la fonction diélectrique de
l’argent cristallin.
Le terme d’amortissement électronique intrabande γ correspond au déphasage des plasmons de volume (amortissement de Landau) qui est typiquement de ∼0.1eV pour la plupart des métaux. Le terme d’amortissement interbande α correspond aux diffusions des électrons
qui est affecté par plusieurs processus comme l’interaction de Coulomb,
l’interaction électron-phonon ou la diffusion des électrons aux
interfaces. Sa valeur dépends beaucoup de l’excès d’énergie des
électrons au-dessus du niveau de Fermi EF et de la température θ. Dans l’approximation du liquide de Fermi il est donné par :
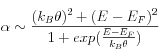
Dans les nanoparticules métalliques, on doit considérer les effets de champ locaux qui induisent une polarisation de surface autour des particules en modifiant fortement leur fonction diélectrique. Si les nanoparticules sont inclues dans un milieu diélectrique ayant une constante ε0, leur réponse peut être décrite dans l’approximation du milieu effectif par une fonction diélectrique de Maxwell-Garnett :
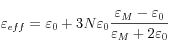
où εM est la fonction diélectrique du métal et N la densité de particules. Une résonance se produit pour la condition εm=-2ℜe(ε0) comme on le voit sur la figure 2. Cette résonance correspond au mode de premier ordre de la diffusion de la lumière par une sphère métallique décrite par la théorie de Mie. On peut aussi l’assimiler à une excitation résonnante de plasmons de surface. La largeur de raie de la résonance de plasmon de surface γeff augmente lorsque la taille des particules diminue. En première approximation, elle est proportionnelle au rapport entre la vitesse des électrons au niveau de Fermi VF et le rayon R des nanoparticules : γeff ∼ VF/R. Pour des particules de très petite taille (typiquement R<2-3 nm), les effets de confinement doivent être pris en considération. Le rayon R est alors remplacé par un rayon effectif qui prend en compte la densité d’états quantiques dans la particule[2]. Des études théoriques récentes de l’amortissement γeff par G. Weick et collaborateurs, a été faite en fonction de la taille des particules et de la température[3] [4]. Un nouveau comportement a été mis en évidence où γeff oscille en fonction de la taille pour des particules de quelques centaines d’atomes. L’origine de cet effet provient des oscillations de la partie radiale ρl de la densité d’états électroniques des états de quasiparticules. Ce comportement est bien reproduit par des calculs numériques extensifs effectués dans l’approximation de la densité locale dépendant du temps (TDLDA).
C2. Dynamique des plasmons de surface dans les nanoparticules de métaux nobles
En raison de la taille réduite des nanoparticules la dynamique des électrons est différente de celle du métal massif. Résumons ces différences en considérant les mécanismes de relaxation qui ont lieu dans un agrégat métallique qui est excité avec des impulsions optiques ultra-brèves à la résonance de plasmon de surface :
♦ Décohérence des plasmons de surface(SP) : Initialement les plasmons de surface excités sont amortis et se désintègrent en quasiparticules en contribuant à une redistribution des électrons autour du niveau de Fermi. Le temps typique de ce processus est celui de l’inverse de la largeur des SP ∼10 fs. Ce mécanisme est plus rapide que dans le métal massif en raison de la diffusion des électrons à la surface de la particule.
♦ Processus de thermalisation électronique : Les quasiparticules se thermalisent pour atteindre une distribution de Fermi Dirac chaude. Comme dans le métal massif ce processus dure quelques centaines de femtosecondes. Cependant il est plus rapide pour des petits agrégats (typiquement pour des particules d’argent il varie entre 200 fs à 300 fs lorsque le rayon des agrégats augmente de 3 à 10 nm). Après la thermalisation la température des électrons peut atteindre environ 1000 degrés deKelvin.
♦ Relaxation électron-réseau : ce mécanisme, comme dans le métal massif, contribue à l’équilibre entre les températures des électrons et du réseau. Il se situe dans une gamme temporelle d’une picoseconde. On peut le décrire avec un modèle à deux températures en supposant que l’on a deux bains couplés (les électrons à la température Te et le réseau à la températute Tlat) qui échangent de l’énergie via le couplage électron-phonon. La dynamique des deux bains est régie par leur inertie thermique respective (chaleur spécifique) et à la propagation dans chacun des bains thermiques.
♦ Dynamique vibrationnelle et transfert d’énergie à la matrice : L’échauffement du réseau est le mécanisme initiateur de la dynamique vibrationnelle des agrégats . Plusieurs modes acoustiques peuvent être excités selon la forme des nanoparticules (un mode de respiration pour une sphère, des vibrations oblate et prolate pour un ellipsoïde …). L’amortissement vibrationel se produit dans une gamme de temps de 100 picosecondes. Lorsque les vibrations s’amortissent un transfert d’énergie entre les agrégats et le milieu diélectrique environnant se produit. Il est plus rapide lorsque la conductivité thermique de la matrice diélectrique est plus grande
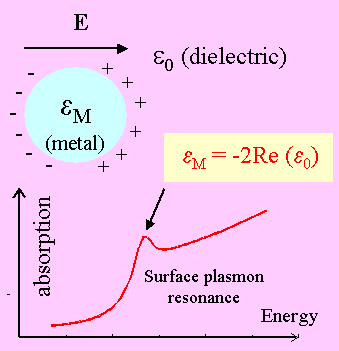
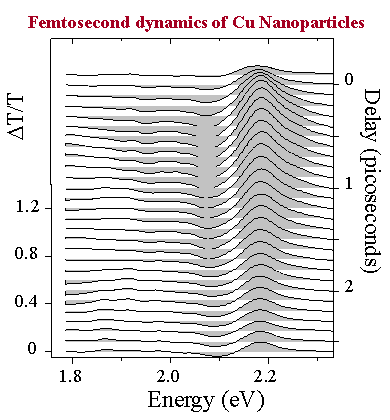
Figure 3 : Dynamique de plasmons de surface dans des nanoparticules de Cu.
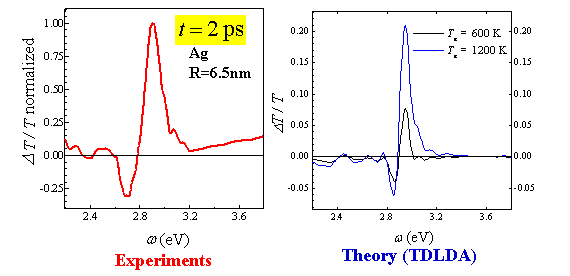
We have studied the above mechanisms by Nous avons étudié les mécanismes ci-dessus en effectuant des expériences pompe-sonde femtosecondes en résonance avec l’absorption des plasmons de surface de nanoparticules de cuivre, d’argent et d’or inclues dans différentes matrices de verre, de SiO2 ou d’Al2O3. Par exemple la dynamique spectro-temporelle des SP dans le cas de nanoparticules de Cu dans du verre (rayon R=5 nm) est montré sur la figure 3. On y voit l’élargissement de la résonance plasmon, la thermalisation des électrons près du niveau de Fermi (sondé par l’intermédiaire des transitions interbandes : bande 3d vers le niveau de Fermi dans la bande de conduction p), et la relaxation électron-réseau[5]. En raison de la proximité du continuum de transitions interbandes (Edp=2.17 eV), la résonance SP (ESP,Cu=2.22 eV) est principalement élargie. Au contraire, dans le cas des nanoparticules d’argent[9] avec un rayon R=6.5 nm, l’énergie de la résonance SP (ESP,Ag=2.85 eV) est bien inférieure à celle des transitions interbandes (Edp=3.99 eV). Le décalage vers le rouge de la résonance SP est ainsi bien plus prononcé que son élargissement (voir la figure 4). La modélisation de ce décalage vers le rouge a été obtenu en effectuant des calculs TDLDA
Figure 4: Surface plasmon dynamics in Ag nanoparticles.
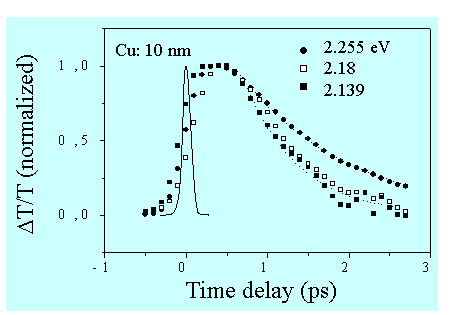
Un aspect intéressant de la dynamique des électrons se produit à la résonance de plasmon de surface. Pendant la relaxation des électrons au réseau, la relaxation est plus lente lorsque l’énergie de sonde se situe à la résonance SP comme on le voit sur la figure 5 dans le cas de nanoparticules de Cu ayant un diamètre moyen de 10 nm (la ligne en pointillé est la corrélation croisée entre les impulsions pompe de 60 fs et celles de la sonde de 10 fs). Il faut se souvenir que, dans de telles expériences pompe-sonde, le caractère collectif des électrons excités par la pompe est très rapidement perdu (quelques dizaines de femtosecondes). Par conséquent, s’est le plasmon excité par la sonde qui est sensible à ce mécanisme de ralentissement. Le mécanisme qui a été proposé pour expliquer ce comportement est que les paires électron-trou peuvent interagir pour émettre un plasmon. Le processus est augmenté par la polarisation de surface des sphères métalliques qui modifie l’écrantage dynamique de l’interaction Coulombienne vue par les électrons dans la nanoparticule. En particulier, cela donne lieu à une diffusion résonante d’un trou de la bande d avec un électron de la bande de conduction avec émission (excitation) d’un plasmon de surface. Lorsque cet effet est pris en compte d’une manière auto-cohérente dans le calcul de la fonction diélectrique, la dynamique de relaxation est plus lente à la résonance de plasmon de nanoparticules de cuivre. Ce mécanisme d’amortissement induit par la surface augmente lorsque la taille des nanoparticules diminue selon la loi suivante :
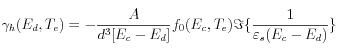
Figure 5 : Transmission dynamique ΔT/T(t) dans des nanoparticules de Cu près de la résonance SP.
où γh est l’amortissement d’un trou qui se recombine avec un électron pour émettre un plasmon, Ec,d sont les énergies des électrons de conduction de bande d, εs est la fonction diélectrique auto-cohérente des plasmons de surface et f0 est la densité d’occupation des électrons. Ce mécanisme est proportionnel à ∼d-3
et devient négligeable pour des nanoparticules dont le diamètre est
plus grand que 20 nm comme cela été observé dans le cas du cuivre. Dans
le cas de nanoparticules d’argent la dynamique est également différente à
la résonance SP comme on le voit sur la figure 6. dans ce cas la
diffusion résonante d’un trou de la bande d ne peut pas se produire car
la résonance SP est loin de la transition interbande. Une explication
possible est alors un ralentissement apparent de la dynamique des
électrons dû à un décalage spectral et à un élargissement de la
résonance.
Un autre processus dynamique intéressant qui a été prédit
mais pas encore observé dans des agrégats de petite taille est
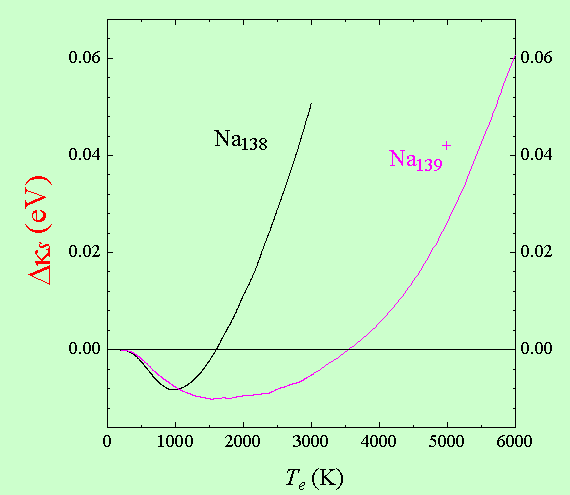
l’existence d’un décalage vers le bleu de la résonance SP lorsque la température augmente. Il est dû à une variation non monotone de l’énergie cinétique spécifique par particule Δκs=κs(Te)-κs(0) en fonction de la température des électrons Te
comme on le voit sur la figure 7 dans le cas d’agrégats de sodium. Pour
pouvoir observer cet effet il faut cependant des agrégats
mono-disperses, de petite taille et inclus dans une matrice ayant une
conductivité thermique importante de façon à ne pas surchauffer les
agrégats et les amener à leur point de fusion. Par définition l’énergie
cinétique Κs est donnée par : Κs = Nκs ≡ Us – ∫VKs(r)ρ(r)dr ; Us étant l’énergie interne totale de l’agrégat, VKs est le potentiel auto-cohérent de Kohn-Sham et ρ est la densité d’électrons dans l’agrégat.
Figure 6 : Dynamique de plasmon surface de nanoparticules d’Ag
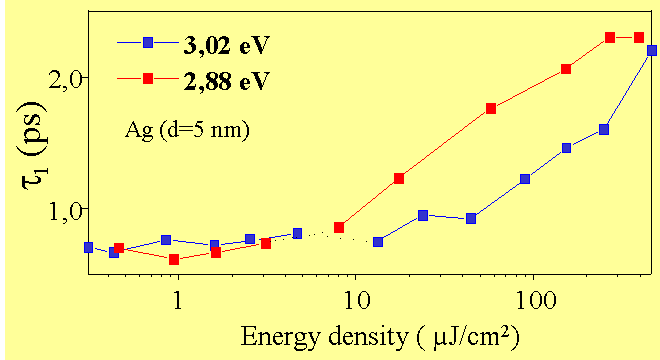
Figure 7 : Dynamique du décalage spectral de SP d’agrégats de Na
C3. Réponse optique de nanostructures métalliques périodiques
Les propriétés optiques de réseaux de trous ou de fentes sont caractérisées par une transmission exaltée dans certaines régions spectrales qui correspondent à l’excitation de plasmons-polaritons de surface. La physique de cet augmentation de transmission peut être comprise en terme de modification de la densité de champ électromagnétique qui se répartie de manière périodique sur le réseau de trous (ou de fentes) via la propagation de polaritons à l’interface métal diélectrique (le diélectrique peut être le substrat ou l’air). Par conséquent la fonction diélectrique du métal joue un rôle important sur la position et la largeur spectrales des pics de transmission (et de réflexion) de la lumière. D’un point de vue théorique, il n’est pas suffisant de considérer simplement une fonction diélectrique de Drude pour le métal mais d’autres contributions à la réponse optique, telles que les transitions interbandes, doivent être prises en considération. Nous avons effectué des études expérimentales de la réponse optique de réseaux de trous nanostructurés dans un film d’or et nous avons effectué des expériences résolues en temps à l’échelle femtoseconde sur ces nanostructures. Les échantillons que nous avons étudiés ont été élaborés dans le groupe de T. Ebbesen au laboratoire ISIS à Strasbourg, par la technique de faisceau d’ions focalisés (FIB). Ils sont constitués de films d’épaisseur 250 nm, déposés sur différents substrats (Al2O3 ou verre), avec différentes périodes de réseaux de trous. La transmission linéaire possède deux pics principaux qui se comporte différemment en fonction de la période du réseau. Le pic aux grandes longueurs d’ondes correspond à l’excitation de plasmons de surface à l’interface métal/substrat. Il se décale vers le rouge lorsque la période de réseau augmente. Dans le domaine spectral 500-600 nm, près de la transition interbande de l’or, une autre résonance est présente qui n’est pas une caractéristique du réseau et qui ne peut pas être interprétée avec une fonction diélectrique de Drude.
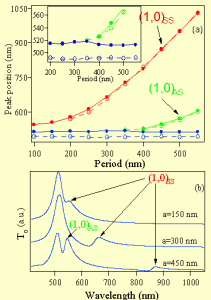
To explain these Pour expliquer ces comportements spectraux ainsi que d’autres aspects particuliers de la réponse optique linéaire, nous avons étudié la réponse théorique de films métalliques structurés périodiquement par des ouvertures sub-longueur d’onde. Notre approche consiste à étudier la diffraction par un réseau uni-dimensionel d’ondes électromagnétiques transverses magnétiques. La méthode que nous utilisons est l’analyse d’ondes couplées (RCWA) qui nous permet de calculer analytiquement les efficacités de diffraction. Les termes d’ordre zéro et un donnent la transmission, la réflectivité et l’absorption de nanostructures symétriques et asymétriques environnées d’un milieu diélectrique soit identique, soit différent. Pour les deux types de nanostructures la forme spectrale de la transmission exaltée associée aux plasmons de surface présente un profil de Fano comme on le voit sur la figure 8. Dans le cas des nanostructures symétriques, nous avons étudié les conditions nécessaires à la formation d’ondes couplées de plasmons-polaritons ainsi que leur effet sur la réponse optique d’une structure modulée (figure 9). Pour les nanostructures asymétriques, nous avons pu expliquer la non-réciprocité de la réflectivité et nous avons également étudié l’influence de la constante diélectrique du milieu environnant sur la transmission exaltée par la nanostructure. Nous avons également utilisé une fonction diélectrique de type Lindhard, calculée par une méthode auto-cohérente, qui prend en compte les électrons de conduction et de cœur.Cela nous a permis d’expliquer pourquoi les résonances associées aux interfaces se déplacent spectralement de façon non-linéaire lorsque la période diminue pour finalement converger au seuil de transition interbande (figure 10). De plus, nous avons démontré l’existence d’une nouvelle résonance (observée expérimentalement) associée exclusivement aux propriétés électroniques du gaz d’électrons des métaux nobles.
Figure 8 : Profil Fano de l’augmentation de transmission d’un réseau de trous dans un film d’Au.
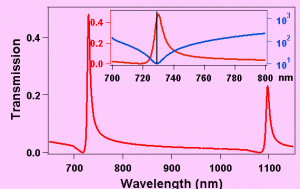
Figure 9 : Couplage entre plasmons de surface d’un réseau unidimensionnel dans un film d’Ag
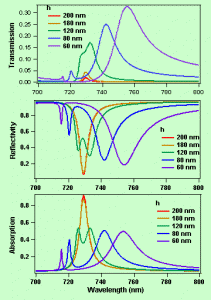
Figure 10 : Modélisation de la transmission de nanostructures d’or près de la transition interbande
Nous avons également étudié les propriétés dynamiques de réseaux de trous en effectuant des expériences de spectroscopie pompe-sonde femtoseconde. L’amplitude et les principaux aspects de la transmission différentielle résolue en temps montrent que la dynamique des nanostructures périodiques est principalement due à la variation temporelle de la fonction diélectrique du métal. Cela a été confirmé par le modèle RCWA. Dans ce cas, nous avons pris en compte la variation temporelle de la fonction diélectrique de l’or via l’augmentation ultra-rapide de la température d’électrons et de sa relaxation au réseau en utilisant le modèle à deux bains thermiques.