C1. Introduction: dielectric function of bulk metals and nanoparticles
The optical response of metals is dominated by two contributions of the electrons to the dielectric function ε(q,ω) = εD(q,ω) + εib(q,ω). εD corresponds to the conduction electrons. It is associated to intraband optical processes (electrons and holes belonging to the same band) that can be described in first approximation by a Drude dielectric function. εib corresponds to interband optical processes which can be described by the Lindhard dielectric function.
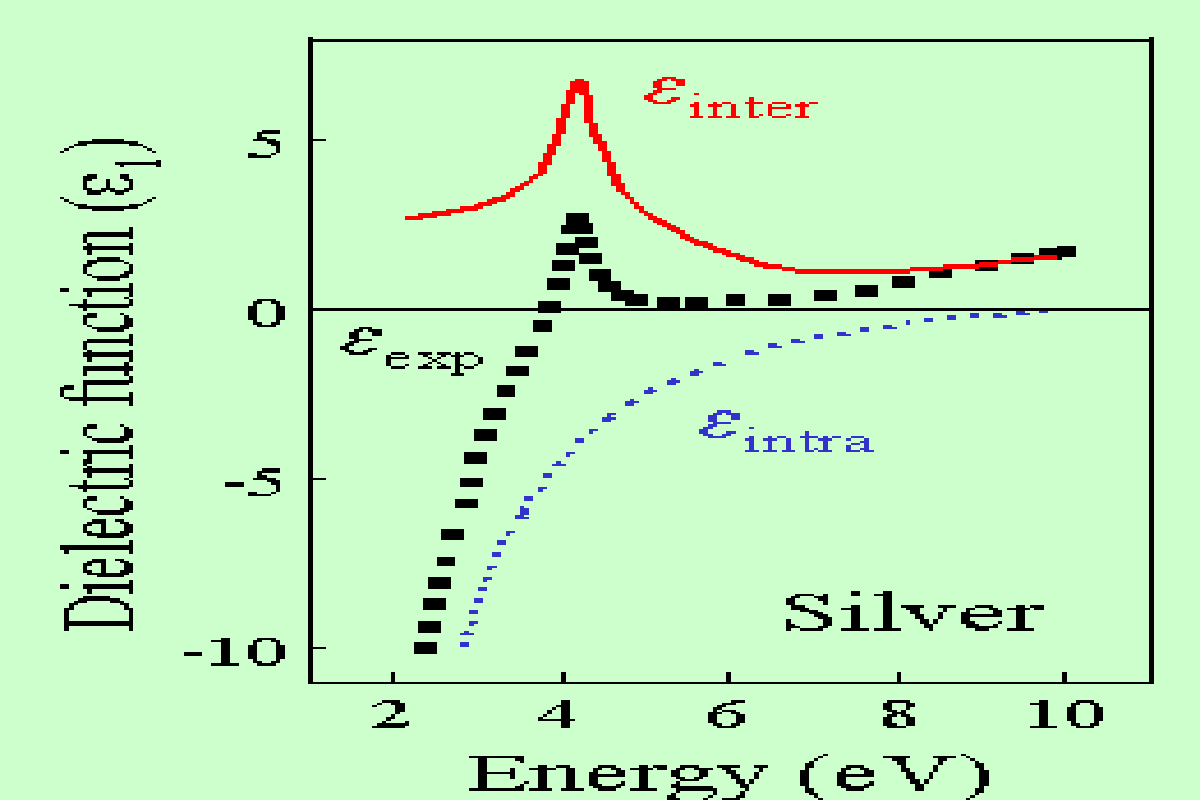
Figure 1 : Dielectric function of Ag.
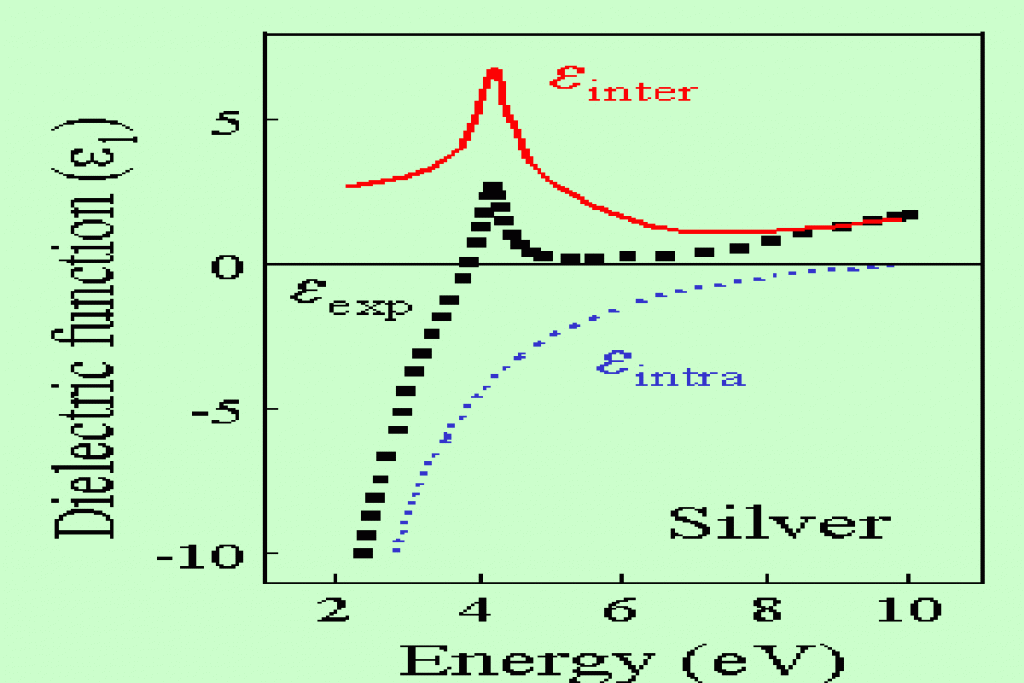
|k,l> electron of wave vector k in the band l; f Fermi Dirac density; hω photon energy. Figure 1 shows an example of the intraband and interband contributions to the bulk dielectric function of Ag.
The intraband electronic damping γ corresponds to the dephasing of the bulk plasmons (Landau damping) which typically is of ∼0.1eV in bulk metals. The interband damping term α corresponds to the scattering of the electrons which is influenced by several processes like the Coulomb interaction, the electron-phonon interaction or the electron scattering at interfaces. Its value strongly depends on the excess energy of the electrons above the Fermi level EF
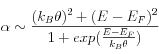
In metallic nanoparticles one has to consider local field effects which induce a surface polarization around the particles that strongly modifies their dielectric function. If the nanoparticles are embedded in a dielectric medium with constant ε0, their response can be described in the effective medium approximation with a Maxwell-Garnett dielectric function:
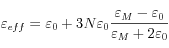
where εM is the metal dielectric function and N the density of particles. A resonance occurs when the condition εm=-2ℜe(ε0) as shown in figure 2. This resonance corresponds to the first order mode of the light scattering by a metallic sphere obtained from the Mie theory. It can also be understood as the resonant excitation of surface plasmons. The line width of the surface plasmon resonance γeff increases when the size of the particles decrease. In first approximation, it is proportional to the ratio of the Fermi velocity VF to the nanoparticle radius R: γeff ∼ VF/R. For small size particles (typically R<2-3 nm), confinement effects have to be taken into account. The radius R is then replaced by an effective one which takes into account the density of quantum states in the particles. Recent theoretical studies of the damping γeff by G. Weick and coworkers, have been made as a function of the size of the particles and temperature. A new oscillatory behavior of γeff as a function of the particle size has been reported for clusters of a few hundreds atoms. Its origin comes from the oscillatory behavior of the radial part ρl of the electronic density of single particle states. This behavior compares satisfactorily with numerical simulations obtained within the time dependent local density approximation.
C2. Surface plasmon dynamics in noble metal particles
Because of the reduced size of metallic nanoparticles the electron dynamics is different than the one occurring in the bulk metal. Let us summarize these differences by considering the electronic relaxation mechanisms that take place in a metallic aggregate which is excited with an ultrashort optical pulse at the surface plasmon resonance:
♦ Decoherence of surface plasmons (SP): Initially the excited surface plasmons are damped and decay into quasi-particle states contributing to a redistribution of the electrons around the Fermi level. The typical time scale is the one of the inverse SP line width ∼10 fs. The process is faster than in the bulk metal because of the surface assisted electron scattering.
♦ Electron thermalization process: The quasiparticles thermalize to a hot Fermi Dirac distribution. Like in the bulk metal this process lasts a few hundreds of femtoseconds. However it is faster for smaller aggregates (typically for silver particles it varies from 200 fs to 300 fs when the radius of the aggregate increases from 3 to 10 nm). The temperature of the electrons reached after the thermalization occurs can be as high as 1000 Kelvin.
♦ Electron-lattice relaxation: This mechanism, like in the bulk metal, contributes to the equilibrium between the electrons and the lattice temperatures. It takes place in the temporal scale of one picosecond. It can be well described by the two temperatures model that assumes two coupled heat baths (the electrons at temperature Te and the lattice at temperature Tlat) exchanging energy via the electron-phonon coupling. The dynamics of the two baths is subject to their respective thermal inertia (specific heats) and to the heat propagation in each sub-bath.
♦ Vibrational dynamics and energy transfer to the matrix: The heating of the lattice is the triggering mechanism for the vibrational dynamics of the aggregates . Several acoustic modes can develop depending on the shape of the nanoparticle (one breathing mode for a sphere, oblate and prolate vibrations for an ellipsoïd…). The vibrational damping occurs in the time scale of 100 picoseconds. While the vibrations damp out an energy transfer to the dielectric medium surrounding the metal aggregates takes place. It is faster when the thermal conductivity of the dielectric matrix is larger.
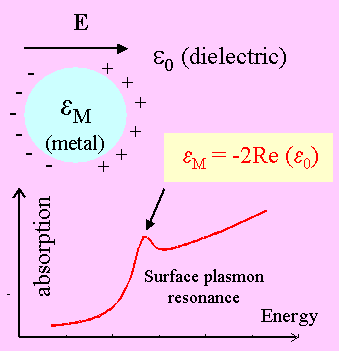
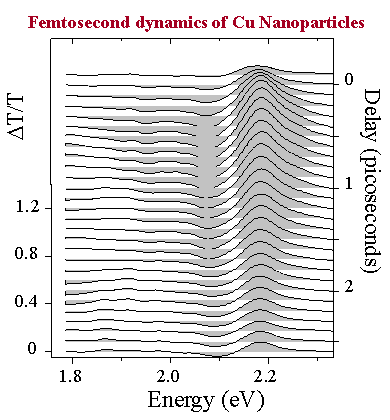
Figure 3 : Surface plasmon dynamics in Cu nanoparticles.
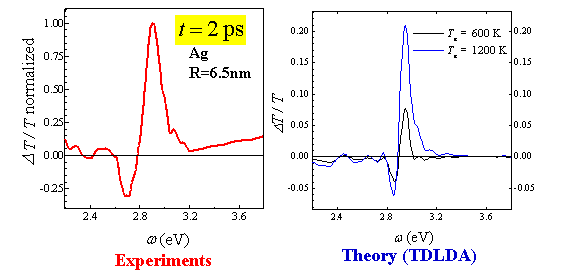
We have studied the above mechanisms by performing femtosecond pump-probe experiments on resonance with the surface plasmon absorption of copper, silver and gold nanoparticles embedded in different matrices made of glass, SiO2 or Al2O3. For example the spectro-temporal dynamics of the SP in the case of Cu nanoparticles in glass (radius R=5 nm) is displayed in Figure 3. It shows the plasmon broadening, the electron thermalization near the Fermi level (probed via the interband transitions from the 3d band to the Fermi level in the p conduction band), and the electron-lattice relaxation. Because of its proximity to the quasi-particle interband continuum (Edp=2.17 eV), the SP resonance (ESP,Cu=2.22 eV) is mainly broadened. In contrast, for silver nanoparticles with a radius R=6.5 nm, the energy of the SP resonance (ESP,Ag=2.85 eV) is much lower than the interband transition (Edp=3.99 eV). The red-shift of the SP is therefore much more pronounced than its broadening (see figure 4). The modeling of this red shift has been made by performing TDLDA calculations
Figure 4: Surface plasmon dynamics in Ag nanoparticles.
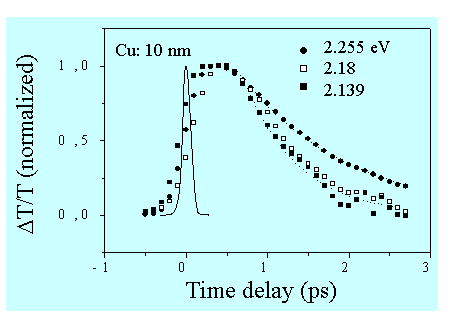
An interesting feature of the electron dynamics occurs at the surface plasmon resonance. During the cooling of the electrons to the lattice, a longer relaxation occurs when the probe energy is at the SP resonance as seen in figure 5 for Cu Nanoparticles with an average diameter of 10 nm (the dotted line is the cross correlation between the 60 fs pump and 10 fs probe pulses). One should keep in mind that, in such pump-probe experiments, the collective character of the electrons excited by the pump is lost very quickly (a few tens of femtoseconds). Therefore, it is the plasmon that is created by the probe which is sensitive to this mechanism. The mechanism that has been proposed to explain this behavior is that electron-hole pairs can interact to emit a plasmon[11]. This process is enhanced by the polarization at the surface of the metallic sphere which modifies the dynamical screening of the electron-electron interactions in the nanoparticle. In particular, it leads to a resonant scattering of a hole in the d band into the conduction band by emission of a plasmon. When this effect is taken into account in a self-consistent manner in the calculation of the dielectric function, the relaxation dynamics is slower at the plasmon resonance of copper nanoparticles. This surface induced damping mechanism increases when the particle size decreases according to :
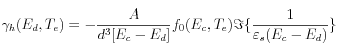
Figure 5 : Transmission dynamics ΔT/T(t) in Cu nanoparticles near the SP resonance.
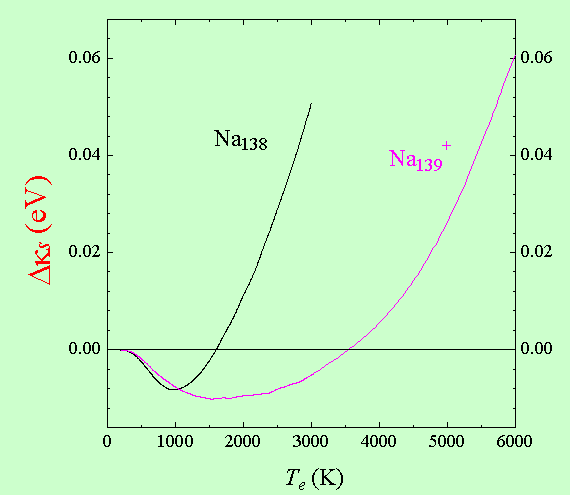
where γh is the decay of a hole that recombines with an electron to emit a plasmon, Ec,d are the electron conduction and d-hole bands, εs is the self-consistent surface plasmon dielectric function and f0 is the occupation density of electrons. This mechanism is ∼d-3 and becomes negligible for particles diameters d larger than 20 nm as observed experimentally in the Cu nanoparticles. In the case of silver nanoparticles. the dynamics is also different at the SP resonance as shown in figure 6. In that case the resonant scattering of the d holes cannot occur because the SP is far below the interband transition. A possible explanation is then an apparent slowing of the electron dynamics due to a combined shift and broadening of the SP resonance. Another interesting dynamical process that is predicted and not yet observed in small clusters is a blue shift of the SP resonance with increasing electron temperature. It is due to a non monotonic change of the specific kinetic energy per particle Δκs=κs(Te)-κs(0) as a function of the electron temperature Te as shown in figure 7 for the case of sodium clusters. To be observed this effect however requires small dispersionless clusters embedded in a highly conductive matrix to prevent the over heating of the clusters lattice temperature. By definition the kinetic energy Κs is given by: Κs = Nκs ≡ Us – ∫VKs(r)ρ(r)dr ; Us being the total internal energy of the cluster, VKs is the Kohn-Sham consistent potential and ρ is the density of electrons in the cluster.
Figure 6 : Surface plasmon dynamics in Ag nanoparticles
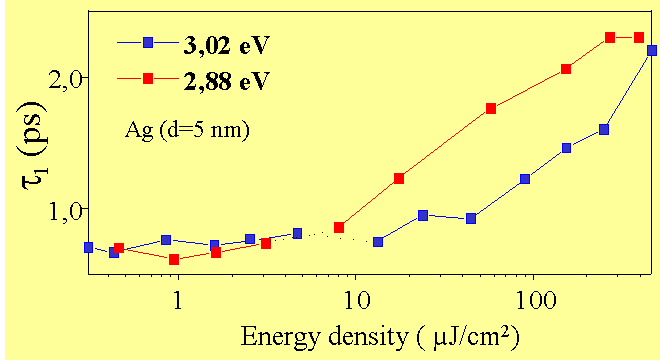
Figure 7 : Dynamical SP shift in Na clusters
C3. Optical response of periodic metallic nanostructures
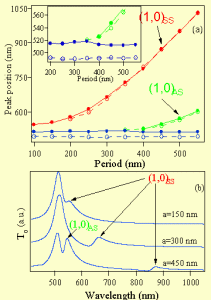
The optical properties of arrays of holes or slits are characterized by an enhanced transmission in certain spectral regions which are related to the excitation of surface plasmons. The physics of this enhancement can be understood in terms of a modification of the density of the electromagnetic field which is periodically sustained over the array by surface polariton waves propagating at the metal dielectric interface (the dielectric can be the substrate on the air). Therefore the dielectric function of the metal plays an important role in the position and width of the transmission (reflection) peaks. From a theoretical point of view it is not enough to consider only a Drude like dielectric function of the metal but other electronic contributions to the optical response, like interband transitions, have to be considered. We have performed systematic experimental studies of the optical response of arrays of nanostructured holes in gold and performed dynamical studies with femtosecond optical pulses. The samples that we studied have been elaborated in the group of T. Ebbesen in Strasbourg by Focused Ion Beam (ISIS, Strasbourg). They are made of 250 nm thin gold films, deposited on different substrates (Al2O3 or glass), with varying periods. The linear transmission displays two main peaks which behave differently as a function of the period of the array. The long-wavelength peak associated to the excitation of the surface plasmon at the metal/substrate interface shifts to the red with an increasing period. In the 500-600 nm spectral range, near the interband transition threshold of gold, another resonance is present which is not a characteristic of the array and that cannot be interpreted with a simple Drude-like dielectric medium.
To explain these spectral behaviors as well as other specific features of the enhanced linear optical response, we have investigated the theoretical response of periodically structured metallic films constituted of sub-wavelength apertures. Our approach consists in studying the diffraction of transverse magnetic polarized electromagnetic waves by a one-dimensional grating. The method that we use is the Rigorous Coupled Waves Analysis (RCWA) allowing us to obtain an analytical model to calculate the diffraction efficiencies. The zero and first order terms allow determining the transmission, reflectivity and absorption of symmetric or asymmetric nanostructures surrounded either by identical or different dielectric media. For both type of nanostructures the spectral shape of the enhanced resonant transmission associated to surface plasmons displays a Fano profile as seen in figure 8. In the case of symmetric nanostructures, we have studied the conditions of formation of coupled surface plasmon-polaritons as well as their effect on the optical response of the modulated structure (figure 9). For asymmetric nanostructures, we have been able to explain the non-reciprocity of the reflectivity and we have also investigated the spectral dependency of the enhanced resonant transmission on the refractive index of the dielectric surrounding the metal film. We have also used a dielectric function calculated by a self consistent field method which takes into account both the conduction and the core electrons. We have been able to explain why the resonances associated to the two interfaces shift non linearly to short wavelengths as the period decreases to finally converge at the interband threshold (Fig. 10). In addition, we have demonstrated the existence of a resonance associated exclusively to the electronic properties of the noble metal
Figure 8 : Fano profile of the enhanced transmission of arrays of holes in Au
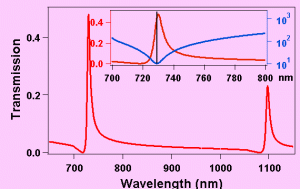
Figure 9 : Coupled surface plasmons in a one dimensionnal Silver array
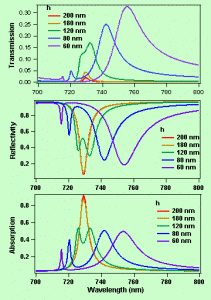
Figure 10 : Modeling of gold nanostructures at the interband transition
We have also studied the dynamical properties of the arrays of holes by femtosecond pump-probe spectroscopy. The amplitude and the main spectral features of the differential transmission have shown that the dynamics of the periodic nanostructures is mainly due to the variation of metallic dielectric function. It has been confirmed by the RCWA model. In that case, we have taken into account the temporal variation of the gold dielectric function via the ultrafast raise of the electron temperature and its relaxation to the lattice temperature using the two temperature model.