A1. Notions fondamentales de magnéto-optique.
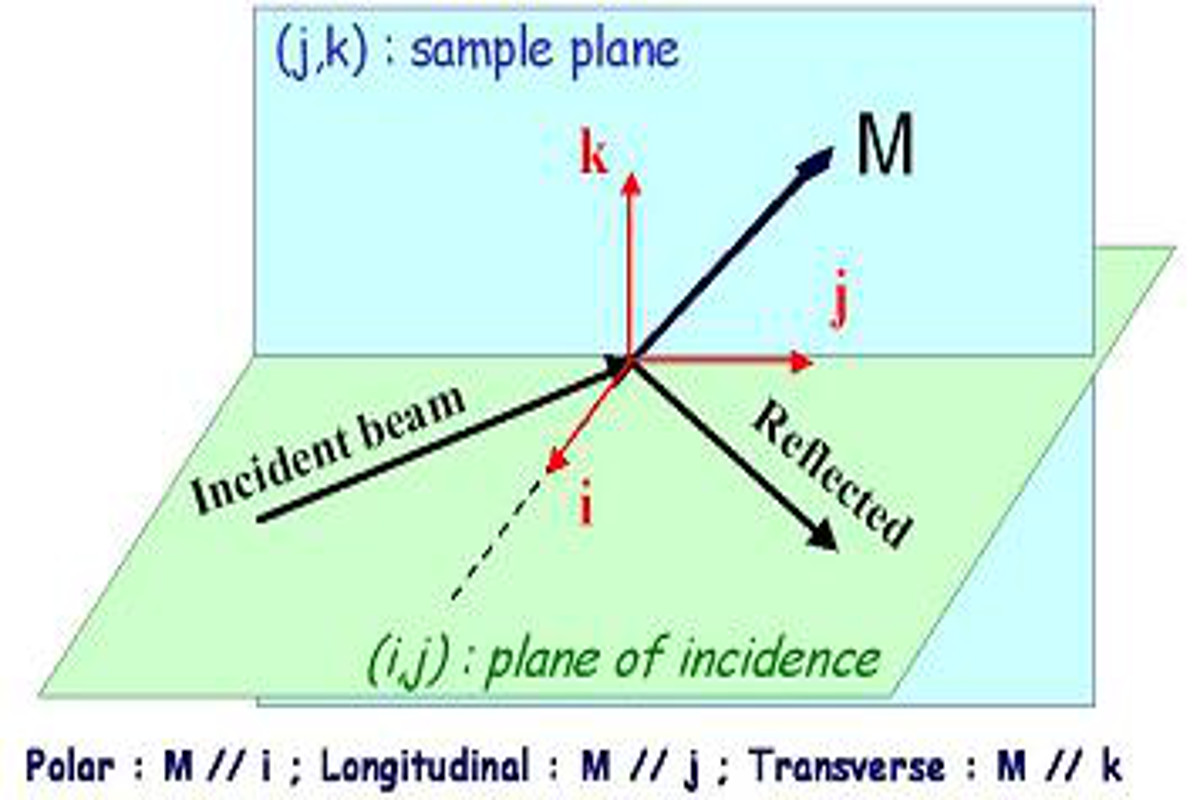
En 1845 Michael Faraday découvrit que la polarisation de la lumière, se propageant au travers d’une substance magnétique, tourne. Cet effet magnéto-optique, d’abord observé en transmission dans un échantillon de verre placé dans un champ magnétique intense puis plus tard dans la réflectivité d’un métal par John Kerr, est maintenant une méthode très utilisée pour étudier les propriétés des matériaux magnétiques. Les effets Kerr et Faraday magnéto-optiques sont dus à une asymétrie de l’absorption et de la réfraction des composantes circulaires droite et gauche de la lumière. Au niveau microscopique, cette asymétrie a son origine dans l’interaction spin-orbite. Dans la théorie de la réponse linéaire, ces effets sont bien décrits par les composantes non-diagonales du tenseur diélectrique complexe εxy. Par exemple, la rotation Kerr θK et l’ellipticité ηK acquises par de la lumière (initialement polarisée linéairement) réfléchie par un matériau ferromagnétique est donnée, en géométrie polaire, par :
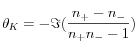
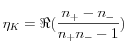
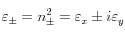
Figure 1 : Configurations Kerr magnéto-optiques.
A2. Pourquoi étudier des matériaux ferromagnétiques avec des impulsions laser ultra-brèves ?
La
rotation et l’ellipticité de l’état de polarisation de la lumière sont
proportionnelles à l’aimantation M (en première approximation). Il est
ainsi naturel d’espérer pouvoir changer l’état d’aimantation d’un
échantillon ferromagnétique en utilisant une impulsion laser intense et
très courte (impulsion pompe) et de pouvoir en mesurer la variation au
moyen d’une deuxième impulsion (sonde) retardée par rapport à la
première. En analysant la rotation et l’ellipticité de la sonde
réfléchie (respectivement transmise) en fonction du retard pompe-sonde τ
on peut ainsi obtenir des informations sur la dynamique ultra-rapide
d’aimantation M(τ). Cet effet Kerr (respectivement Faraday) magnéto-optique résolu en temps est la base de ce que nous appelons Femtomagnétisme, c’est à dire la dynamique d’aimantation à l’échelle femtoseconde.
En utilisant une telle approche, on peut obtenir des informations sur
les processus magnétiques qui ne sont pas accessibles autrement avec les
méthodes conventionnelles utilisant des champs magnétiques
impulsionnels. La possibilité d’explorer les mécanismes de relaxation se
produisant dans les métaux magnétiques avec une résolution temporelle
femtoseconde offre de nouvelles perspectives.
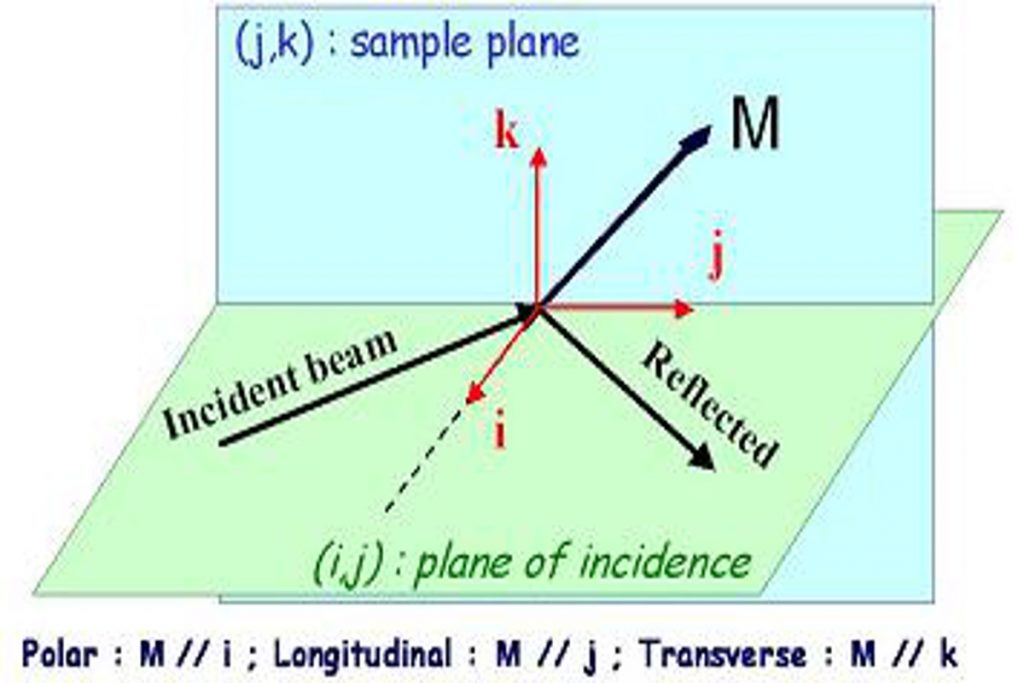
D’un point de vue fondamental, on peut par exemple étudier les changements dynamiques de l’anisotropie magnétique ou bien la dynamique de l’interaction d’échange
(région en rouge sur la fig.2). Il est également possible d’explorer en
temps réel la précession de l’aimantation autour du champ effectif
ainsi que l’amortissement de cette précession (région en bleu sur la
fig.2).
D’un point de vue des applications, on peut
envisager développer de nouveau dispositifs magnétiques ultra-rapides
qui peuvent être entièrement contrôlés par des impulsions lumineuses.
C’est la base d’un nouveau champ de recherche et de développement appelé
Photonique de Spins dont l’objectif est de pouvoir modifier et
contrôler et mesurer l’aimantation de systèmes magnétiques en utilisant
des photons.
Figure 2 : Processus de relaxation en magnétisme.
A3. Dynamique d’aimantation ultra-rapide : Femtomagnétisme.
L’absorption d’une impulsion laser ultra-brève dans un métal se produit par des transitions optiques interbandes et and intrabandes. Les transitions intrabandes correspondent à l’excitation d’une excitation collective (un plasmon)
qui se désintègre rapidement en quasiparticules. La densité d’états
électroniques occupés qui en résulte est très fortement perturbée avec
des électrons présents bien au-dessus du niveau de Fermi EF ainsi que des états vides (trous) en dessous de EF. L’interaction de Coulomb entre les états excités de quasiparticules contribue à une redistribution des électrons et trous. Ce processus de thermalisation
dure quelques centaines de femtosecondes et contribue à l’établissement
d’une distribution de Fermi Dirac qui possède une température
électronique Te qui peut atteindre plusieurs centaines de degrés Kelvin, selon le nombre de photons absorbés.
Un mécanisme efficace de relaxation d’énergie est l’interaction électron-phonon.
Pendant une gamme de temps de l’ordre de 1 ps, la distribution chaude
d’électrons se refroidit en cédant de l’énergie au réseau cristallin
dont la température Tl augmente jusqu’à ce
que l’équilibre entre les températures électronique et de réseau soit
atteint. Ce processus de relaxation est qualitativement bien décrit par
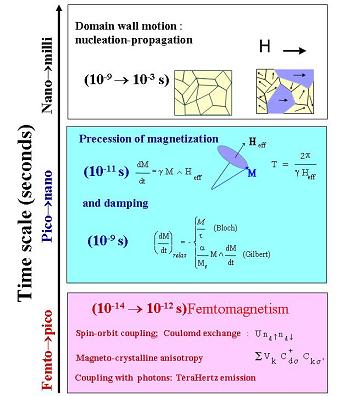
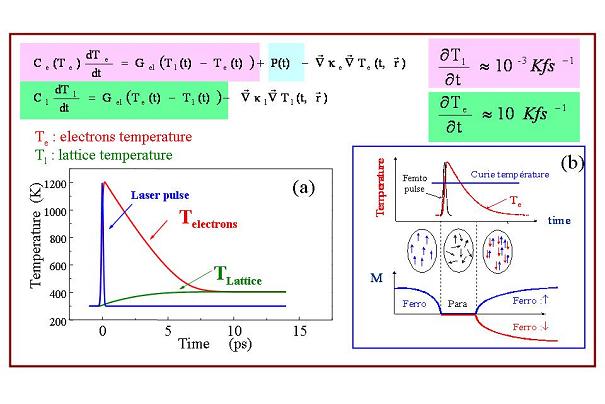
le modèle à deux températures montré sur la fig. 3(a). Les équations de la chaleur décrivant les deux bains aux températures Te and Tl sont couplées par l’interaction électron-phonon (considérée ici comme une constante Gel) et l’inertie thermique de chacun des deux bains est donnée par leur chaleur spécifique Ce pour les électrons et Cl pour le réseau.
Figure 3 : Modèle à deux températures. (a) : relaxation électron-réseau. (b) désaimantation ultra-rapide induite par une impulsion laser.
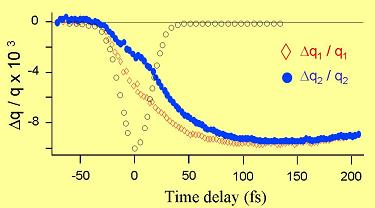
Deux questions importantes ont été soulevées concernant la désaimantation ultra-rapide. Quel est le temps le plus court pendant lequel la désaimantation a lieu ? et deuxièmement quel est le mécanisme qui est impliqué ? Nous avons pu répondre à la première de ces questions en effectuant des études détaillées du tenseur magnéto-optique dépendant du temps avec des impulsions laser de 20 fs de durée. L’expérience fut réalisée avec des films de CoPt3 en mesurant en fonction du retard pompe-sonde l’ellipticité et la rotation Kerr d’une impulsion sonde de 20 fs, à 800 nm, ayant initialement une polarisation linéaire. On peut alors montrer que, connaissant à la fois les composantes statiques et dynamiques de l’ellipticité, de la rotation, de la réflectivité et de la transmission de l’échantillon, on peut obtenir les composantes diagonales et non-diagonales du tenseur de susceptibilité magnéto-optique complexe. De plus il est possible d’en extraire les composantes complexes du vecteur de Voigt q=q1+iq2 qui est la quantité proportionnelle à l’aimantation.
Les résultats, montrés dans la figure 5, montrent clairement que q1 et q2 ne suivent la même dynamique qu’après un temps de quelques dizaines de femtosecondes. Le même comportement est observé en effectuant des mesures Faraday résolues en temps. De plus, la constante de temps correspondant à la désaimantation correspond exactement au temps de thermalisation des électrons. Ce temps, qui est obtenu à partir de mesures de transmission et de réflectivité résolues en temps, est de 60 fs. Par conséquent, la désaimantation se produit pendant une durée correspondant à la redistribution des quasiparticules (électrons et trous) autour du niveau de Fermi. Soulignons que pendant cette gamme de temps la température de réseau Tl est fortement hors équilibre avec celle des électrons Te (voir la figure 3 ci-dessus).
Figure 5 : Dynamique d’aimantation ultra-rapide dans CoPt.
En ce qui concerne le mécanisme physique impliqué dans la désaimantation la question fondamentale qui se pose est : Où va la perte de moment angulaire associée à la désaimantation (renversement de spins) ? Bien qu’il reste des questions théoriques non encore résolues concernant ce point, l’interaction spin-orbite est vraisemblablement un mécanisme important pour induire les retournements de spins entre les populations hors équilibre N+ et N– qui résultent de l’excitation laser femtoseconde. Des études ont également montré la possibilité d’une émission TéraHertz associée à la désaimantation. Des processus de diffusion des spins avec en interaction avec des phonons, similaires aux processus de type Elliot-Yafet dans les semiconducteurs, ont également été mis en avant comme processus de spin-flips.
A4. Précession d’aimantation induite par des impulsions laser femtosecondes
Récemment
il a été montré que, dans certaines configurations, le processus
initial de désaimantation ultra-rapide est suivi d’une ré-aimantation
dont la trajectoire est un mouvement précessionnel. Ce
comportement est en quelque sorte similaire à la résonance
ferromagnétique classique (FMR) induite par un champ magnétique
radio-fréquence.
En utilisant les techniques Magnéto-optiques Kerr et Faraday,
nous avons étudié la dynamique de ré-aimantation de films
ferromagnétiques ainsi que l’influence de la dynamique d’anisotropie sur
la façon dont le mouvement précessionnel commence et se développe.
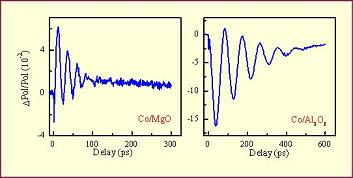
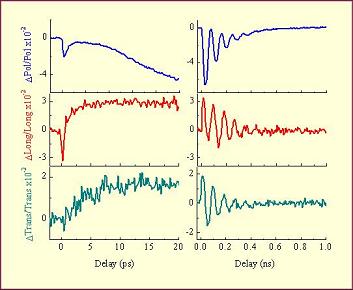
Une description complète de la dynamique du vecteur aimantation M nécessite de déterminer ses trois composantes spatiales. Nous avons mis au point une nouvelle méthode, permettant de mesurer séparément les composantes polaire, longitudinale et transverse de M. Cela nous permet de visualiser la trajectoire du vecteur aimantation jusqu’à 1 ns avec une résolution temporelle donnée par la durée des impulsions laser c. à. d. 120fs pour notre expérience. La figure 6 montre les trois projections de la variation relative de l’aimantation, obtenue avec un film mince de Co/Al2O3. On y voit la diminution rapide des composantes polaire et longitudinale, alors que la composante transverse reste inchangée pendant cette gamme de temps (<1ps). Cela signifie qu’initialement une désaimantation ultra-rapide se produit (le module du vecteur aimantation diminue) et que l’aimantation reste dans le plan xOy (polaire/longitudinal). De plus, comme les amplitudes des composantes polaire et longitudinale varient différemment, une rotation de M a lieu dans le plan xOy. Aux temps longs (jusqu’à 1 ns), un mouvement de précession se développe, avec une période de 25 ps pour un champ statique de 3 kOe appliqué à un angle de 15° par rapport à la normale au plan du film. Cette précession s’amortit en 300 ps.
Figure 6 : Signaux Kerr différentiels polaire, longitudinal, transverse aux temps courts (à gauche) et longs (à droite).
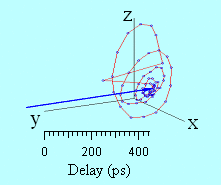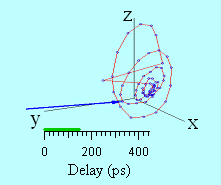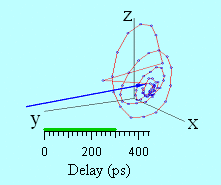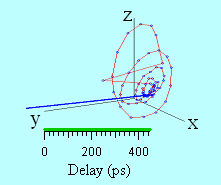
Une représentation tri-dimensionnelle de la trajectoire d’aimantation obtenue à partir des mesures expérimentales est montrée sur la figure 7. L’animation représente la trajectoire dynamique du vecteur aimantation. On y voit successivement la décroissance ultra-rapide de M aux temps courts (100 fs), puis la ré-aimantation partielle du module de l’aimantation qui tourne simultanément dans le plan polaire longitudinal. Enfin la précession a lieu et s’amortie.
Figure 7 : Trajectoire tri-dimensionnelle de l’aimantation mesurée sur CoPt
A5. Influence de l’anisotropie magnéto-cristalline sur la précession de l’aimantation
Une
question importante qui se pose est de savoir quels sont les mécanismes
responsables de la réorientation spatiale du vecteur M ?
Nous avons montré que la rotation d’aimantation qui se produit au cours de la première picoseconde est due à une variation ultrarapide de l’anisotropie magnéto-cristalline . Cette variation est due à l’augmentation de la température électronique via l’interaction spin-orbite. De plus, le champ démagnétisant (lié à l’anisotropie de forme) varie également en fonction de la température,
puisqu’il est proportionnel à l’aimantation qui elle même dépend de la
température. Par conséquent, il y a compétition entre ces deux sources
de réorientation de l’aimantation qui donne lieu à des comportements
dynamiques différents selon le matériau ferromagnétique considéré.
Nous avons étudié deux films de cobalt différents dont les anisotropies magnéto-cristallines sont orthogonales. Le premier film, élaboré par épitaxie par jet moléculaire sur un substrat d’Al2O3, possède une épaisseur de 15 nm et une anisotropie magnéto-cristalline perpendiculaire au plan du film. Le deuxième film de cobalt est plus épais (50 nm). Il est déposé également par MBE sur un substrat de MgO. Il possède un axe d’anisotropie magnéto-cristalline dans le plan du film. La figure 8 montre la comparaison entre les dynamiques aux temps longs pour les deux échantillons. Remarquons le déphasage de π entre les oscillations. Il est dû à une variation ultra-rapide de température qui induit une modification dynamique de l’anisotropie magnéto-cristalline perpendiculaire ou parallèle au plan du film. Il en résulte une rotation du champ effectif soit vers le plan du film soit vers la normale au plan du film. La période de précession est plus courte pour le film de Co/MgO (24 ps). Cela est dû à l’anisotropie très importante pour ce film et donc a un module de champ effectif plus élevé.
Figure 8 : Comparaison entre deux films de cobalt ayant des orientations différentes de l’anisotropie magnéto-cristalline.