A1. Fundamentals of magneto-optics.
In 1845 Michael Faraday discovered that the polarization of light propagating through a magnetized substance is rotated. This magneto-optical effect, first observed in a sample of glass placed in an intense magnetic field and later in the reflectivity of metals by John Kerr, is now a widely used physical method to explore the properties of magnetic materials. The magneto-optical Kerr and Faraday effects are due to an asymmetric absorption and refraction for the left and right helicities of circularly polarized light due to the spin-orbit interaction. In the linear response theory these effects are well described by the off-diagonal complex dielectric tensor element εxy. For example, the Kerr rotation θK and ellipticity ηK acquired by a linearly polarized light reflected from a ferromagnet is given, in the polar geometry, by :
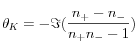
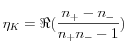
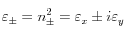
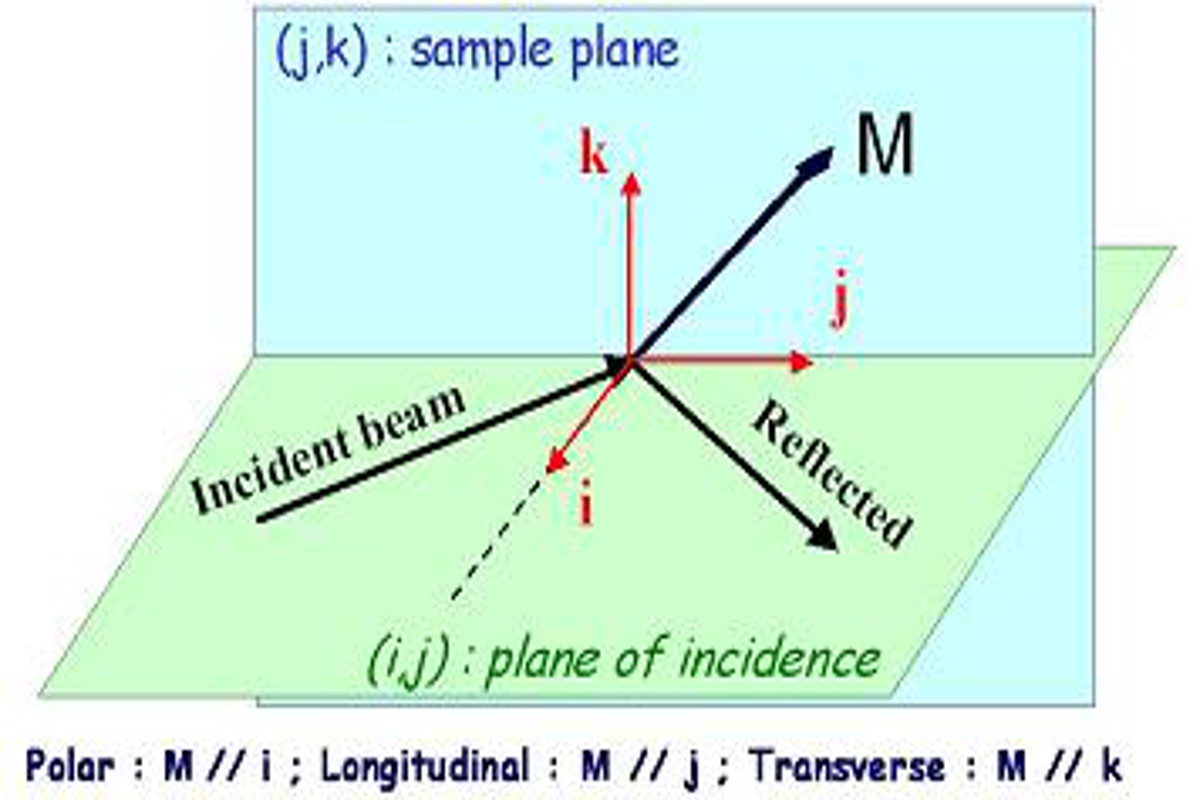
Figure 1 : Kerr magneto-optical configurations.
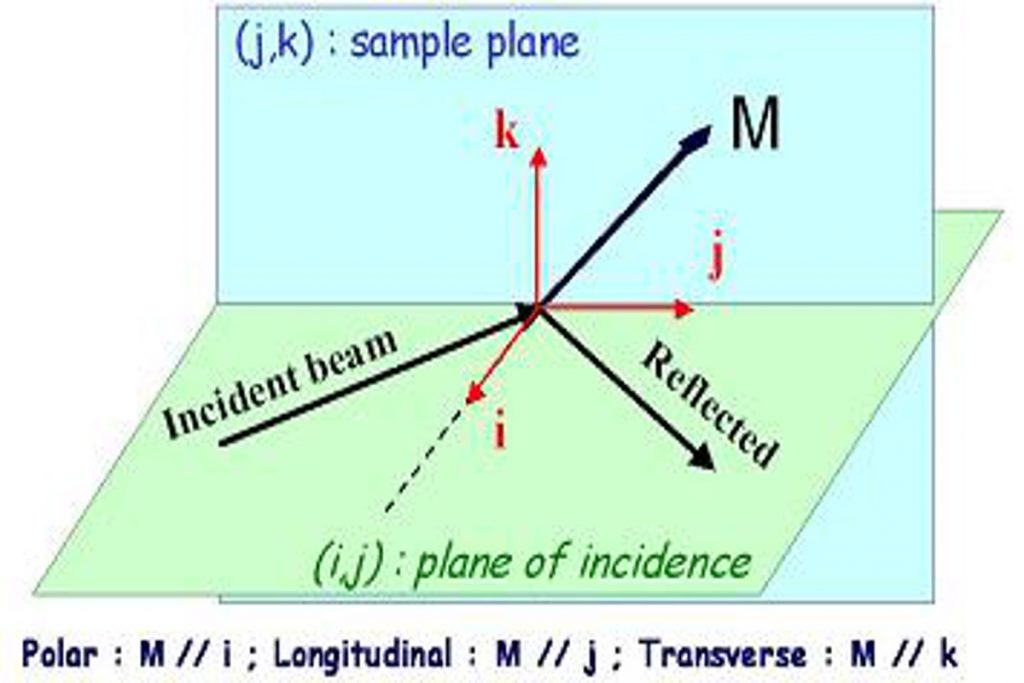
A2. Why studying ferromagnetic materials with ultrashort laser pulses ?
The rotation and ellipticity of the reflected light polarization is proportional to the magnetization M (to first order). It is therefore straightforward to modify the magnetic state of the ferromagnetic sample with an intense femtosecond pump pulse and to measure its magnetization with a delayed probe pulse. By analyzing the rotation and ellipticity of the reflected (respectively transmitted) probe beam as a function of the pump-probe delay τ one can obtain information about the ultrafast magnetization dynamics M(τ). This time resolved pump-probe magneto-optical Kerr (respectively Faraday) effect is the basis of Femtomagnetism i.e. the dynamics of the magnetization at the femtosecond time scale.
Using such approach, one can obtain information on magnetic processes that are not accessible with conventional dynamical studies of the magnetization using a pulsed magnetic field. The possibility of exploring relaxation mechanisms occurring in magnetic metals with a femtosecond temporal resolution opens new possibilities.
From a fundamental point of view, one can study for example the dynamical changes of the magnetic anisotropy or the dynamics of the exchange interaction (red area in fig.2). It is also possible to explore in real time the precession and damping of the magnetization around the effective field (blue area in fig.2).
From an applied point of view, one could envisage designing new ultrafast magnetic devices that can be controlled with light pulses. This is the basis of an emerging applied research field named Spin Photonics which purpose is to modify and control magnetic systems with photons.
Figure 2 : Relaxation processes in magnetism.
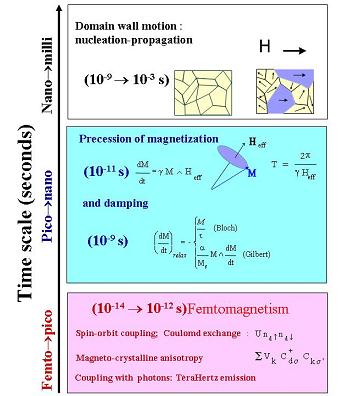
A3. Ultrafast magnetism / Femtomagnetism
The absorption of an ultrashort light pulse in a metal occurs by interband and intraband optical transitions. To the intraband transitions one can associate collective excitations (plamons) which rapidly decays into quasiparticles (electrons and holes). The density of occupied states which results from this process is strongly perturbed out of equilibrium with electrons far above the Fermi level EF as well as with holes below EF. The Coulomb interaction between the excited quasiparticles contributes to a redistribution of the electrons and holes. This process of thermalization lasts a few hundred of femtoseconds, depending on the density of excited quasiparticles. It contributes to the establishment of a new equilibrium with a corresponding hot Fermi-Dirac distribution with a temperature Te that can reach a few thousands Kelvin, depending on the laser energy density.
An efficient mechanism for the relaxation of energy is the electron-phonon interaction. During a time scale of the order of 1 ps, the hot electron distribution cools down giving energy to the crystal lattice which temperature Tl increases until both electronic and phonon baths have the same equilibrium This process is qualitatively well described by the two temperatures model as shown in fig. 3(a). The heat equations describing the two baths at temperatures Te and Tl are coupled by the electron-phonon interaction (taken here as a constant Gel) and the thermal inertia of each bath is given by their respective specific heats, Ce for the electrons and Cl for the lattice.
Figure 3 : Two temperatures model. Top: coupled heat equations, bottom: (a) electron lattice relaxation. (b) ultrafast demagnetization induced with a laser pulse.
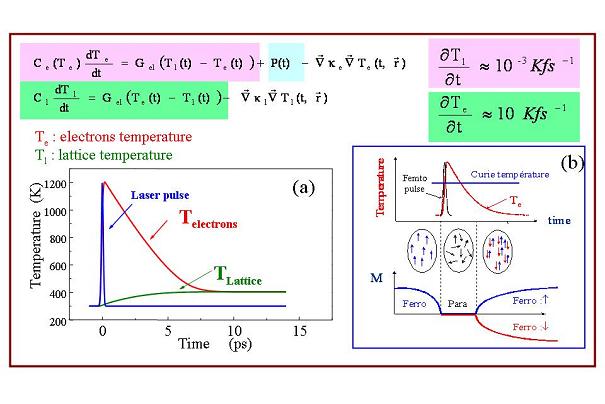
The principle of femtomagnetism is to take advantage of the ultrafast increase of electron temperature induced by a femtosecond laser pulse to change the occupied up (N+) and down (N–) spin states of a magnetic metal so that the magnetization M is modified.
M=(N+-N–)/(N++N–)
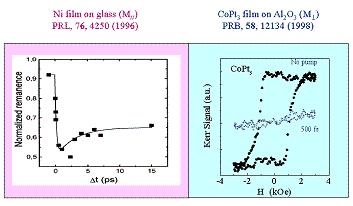
In the case of a ferromagnetic material this process can be used to heat the metal near the Curie temperature so that a full demagnetization occurs in a timescale of a few hundreds of femtoseconds. Such ultrafast demagnetization has been first demonstrated in Nickel films having an in-plane magnetization and later on in CoPt3 films with a perpendicular magnetization (see figure 4)
Fig 4: Femtosecond demagnetization of Ni and CoPt3 films.
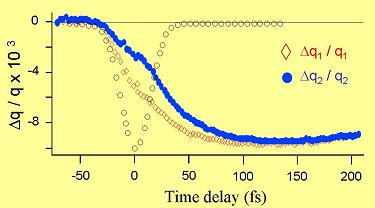
Two important questions have been raised regarding the ultrafast demagnetization. What is the shortest time during which the demagnetization process occurs ? and second what is the physical mechanism involved ? We answered the first one by performing a detailed experimental study of the time dependent magneto-optical tensor using optical pulses with a duration of 20 fs . The experiment was carried out in CoPt3 films by measuring the Kerr ellipticity and rotation of a linearly polarized probe beam of 20 fs at 800 nm as a function of the pump-probe delay. In such case, it can be shown that, knowing the static and dynamical ellipticity and rotation of the polarization, one can retrieve the complex diagonal and non-diagonal magneto-optical tensor elements by using a proper transformation. Moreover, one can deduce the complex Voigt vector q=q1+iq2 which is proportional to the magnetization.
The results, displayed in figure 5, clearly show that both q1 and q2 follow the same dynamics only after an elapse time of a few tens of femtoseconds. The same behaviour is obtained when performing time resolved Faraday measurements. In addition, the demagnetization time constant corresponds exactly to the thermalization time of the electrons as can be deduced form time resolved transmission and reflectivity measurements (60 fs fitted to an exponential relaxation). The conclusion is straightforward : the demagnetization occurs in a time scale during which the quasiparticles (electrons and holes) redistribute near the Fermi level. It is important to emphasize that in such time scale the lattice temperature Tl is completely out of equilibrium with the electron temperature Te (see fig. 3 above).
Figure 5 : Ultrafast magnetization dynamics in CoPt.
Regarding the involved physical mechanism, the fundamental question to answer is : where does the loss of angular momentum associated to the demagnetization (spin flips) go ? Although there are still some non-answered theoretical issues, the spin orbit interaction is one of the favourite candidate as a mechanism for inducing spin flips between the highly non equilibrium N+ and N– spins distributions that follow the absorption of the ultrashort laser pulse. Some experiments have also shown the contribution of a TeraHertz emission associated to the demagnetization. Spin scattering processes with impurities or phonons have also been put forward to explain spin flips similar to the Elliot-Yafet interaction in semiconductors.
A4. Magnetization precession induced by femtosecond laser pulses
It has been shown that in certain configurations, the recovery of the magnetization triggered by the laser pulse follows a precessional pathway. It is somehow similar to the classical ferromagnetic resonance (FMR) induced with radiofrequency magnetic fields except that the inital perturbation is a change of orientation of the effective field induced by the laser heating process.
Using Ultrafast Magneto-Optical Kerr and Faraday techniques, we have studied the spin dynamics of ferromagnetic thin films and nanostructures as well as the influence of the dynamical anisotropy on how the magnetization precession starts and develops.
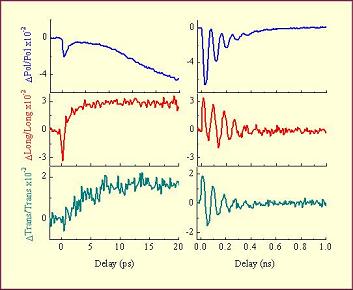
A full description of the dynamics of the magnetization vector M requires to determine its three components in the real space. We have implemented a new measurement method, to separate the polar, longitudinal and transverse Kerr components of M. It allows us retrieving the pathway of the magnetization vector up to 1 ns with a temporal resolution given by the optical pulses (120 fs). Figure 6 shows the three projections of the relative variation of the magnetization after the excitation with a 120 fs laser pulse, obtained on a thin film of Co/Al2O3. It shows the fast decrease of the polar and longitudinal components of the magnetization, while the transverse component remains unchanged during this period (<1ps). This means that initially an ultrafast demagnetization occurs (the modulus decreases) and that the magnetization remains in the xOy plane. In addition, since the amplitudes of the polar and longitudinal differential signals vary differently, a rotation in the xOy plane takes place. At longer time delays (up to 1 ns), a motion of precession develops, with a period of 25 ps for a static field of 3 kOe applied at 15° with respect to the normal (polar) direction. It is damped out in 300 ps.
Figure 6 : Polar, longitudinal, transverse differential Kerr signals: short (left) & long (right) delays.
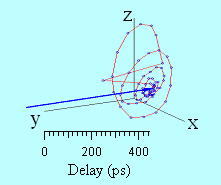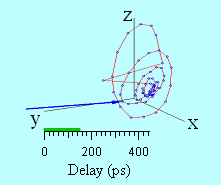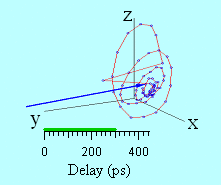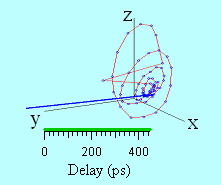
A 3D representation of the magnetization trajectory obtained from the experimental measurements is displayed in figure 7. The animation represents the dynamical trajectory of the magnetization vector. One can see the ultrafast decrease of M at short temporal delays, followed by its partial recovery and its subsequent precession motion and damping.
Figure 7 : Three dimensional animation of the measured magnetization trajectory
A5. Influence of the magnetocrystalline anisotropy on the precession of the magnetization M
An important question is to know what are the mechanisms responsible for the spatial re-orientation of M?
We have shown that the rotation of the magnetization which takes place during the first picoseconds is due to an ultrafast change of the magneto-crystalline and shape anisotropies. It is related to the increase of the electron temperature via the spin-orbit interaction. In addition, the demagnetizing field (or shape anisotropy) also varies with the temperature, because it is proportional to the magnetization which itself changes with the temperature. As a consequence, there is a competition between these two sources of magnetization re-orientation that leads to different dynamical behaviours depending on the particular ferromagnetic material (importance of anisotropy and shape of the structure).
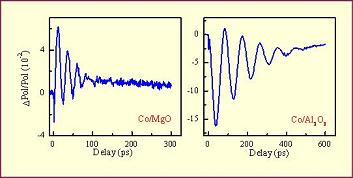
We have studied two different cobalt thin films with two orthogonal orientations of the magneto-crystalline anisotropy. For one of them, grown by molecular beam epitaxy on a Al2O3 substrate, the magnetocrystalline anisotropy is normal to the sample plane. The second sample is a thicker cobalt film (50 nm) grown on MgO substrate. Its easy magnetization axis lies in the plane of the film. Figure 8 displays the comparison between the long delay dynamics for the two selected samples. A π phase shift occurs between the two precession dynamics. It is a consequence of the ultrafast raise of temperature which induces a change of the magnetocrystalline anisotropy either in or perpendicular to the sample plane. It results in a rotation of the effective field either towards the normal to the sample, or towards the sample plane. Note the shorter period of the oscillations (24 ps) observed for the Co/MgO sample. It is due to the large anisotropy field.
Figure 8 : Comparison between two cobalt films with different orientations of the magnetocrystalline anisotropy.