- By atomic-scale modeling one intends the study of materials based on the notion of atomic (and electronic) degrees of freedom, giving access to three basic set of information: a) the description of the electronic structure for a given set of atomic coordinates, b) the optimization of the atomic structure under the action of forces directly derived from the electronic structure and c) the time evolution of the atomic coordinates to ensure proper account of the thermal effects, this evolution resulting (as in point b)) from electronically-derived forces among the atom. These three steps are combined within a unique and self-consistent computational scheme by relying on the so-called first-principles molecular dynamics (FPMD). FPMD succeeds in providing structural, electronic and dynamical properties at finite temperatures as time averages (i.e. statistical averages in the ergodic limit) without employing adjustable parameters extracted from experimental data. Such technique is the common denominator of the atomic-scale modeling activities currently in progress at the DCMI department.
- FPMD is deeply rooted into two conceptual sources having drastically different meanings. On the electronic structure side, FPMD is based on density functional theory (DFT) that allows manageable and yet very accurate access to bonding properties. All the electrons present in the (many-body) system are globally treated as a density distribution expressed as
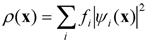
- where ψi(x) are the single-electron wavefunctions and fi the occupation numbers (fi = 1 for each occupied orbital). This framework is the key ingredient to obtain reliable interatomic forces that give access to the temporal evolution of a given configuration, taking place according to the law of statistical mechanics. Overall, the FPMD approach establishes the link between microscopic variables (i.e. based on atomic and electronic degrees of freedom) and macroscopic (experimentally measurable) properties. In addition, direct observation of the mechanisms regulating the atomic movement, made possible by FPMD, provides a fundamental complement to experiments and allows to access pieces of information not accessible to experimental probes.
- We use two versions of FPMD. In the first (Car-Parrinello (CP) method) the electronic orbitals become a dynamical variable that follows adiabatically and self-consistently the ionic motion. In the second (Born-Oppheneimer (BO) method), the electronic structure is fully optimized at each atomic configuration during its time evolution. To ensure adiabatic coupling, the Car-Parrinello method works best for systems having a sizeable gap in the electronic density of states. Accordingly, the use of the BO approach is best suited to handle metallic systems (see below for further strategies to handle these cases).
- The mere application of the FPMD ideas does not allow to describe activated processes that occur on time scales well beyond those currently accessible (say, 100-500 ps at most for systems made of 100-500 atoms) to modern computers. For these reasons, FPMD can be used in conjunction with schemes able to accelerate sampling in the configurations phase space. Within our team, we employ the metadynamics and the blue moon approaches to sample the free energy landscape spanned by a set of reaction coordinates suitable to describe all the slowly varying degrees of freedom. Overall, this amounts to following the dynamical evolution of topological and chemical reactions, in the framework of the so-called “reactive” FPMD.
- Electronic excitations characterized by well defined values of the electronic temperature can be described within an extension of FPMD that relies on the concept of the free energy (FEMD) to describe electronic occupations depending on temperature. In this case the electronic degrees of freedom are not kept on the ground-state BO surface (and do not evolve adiabatically as in the CP method) but are assigned a given temperature, which translates into a Fermi-Dirac distribution of the occupation numbers assigned to each electronic orbital. Specifically, the electron density distribution, for which equation (1) above still holds, but the occupation of the orbitals becomes
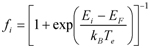
- where Ei is the eigenvalue (energy) of the corresponding eigenfunction (orbital) ψi(x), EF the Fermi level of the system, kB the Boltzmann’s constant and Te the electronic temperature (excitation). In this scheme, the ionic structure evolves then under the action of forces computed self-consistently from the FEMD functional, adjusting to the electronic excitation.
- A strategy that features different degrees of accuracy in the description of the interatomic forces depending on the location in space of specific parts of the system has been shown to be computationally convenient and technically feasible. This is particularly true for very large molecular complexes. The idea consists in identifying a smaller and yet chemically crucial subset of atoms composing the system to be treated within FPMD techniques, the rest of the system being the object of a phenomenological description of the interactions (effective potentials not depending explicitly on the electronic structure). This approach is called quantum mechanics/molecular mechanics (QM/MM) and is currently used within DCMI to investigate large molecular assemblies and the relevant chemical reactions taking place therein.
Contacts :

