Nanoparticles
J.-L. Gallani & B. Donnio
The ex nihilo magnetism of gold and several other metals such as Ag, Pt, Pd, Cu remains poorly understood. Its origin is obscure and debated, and its behaviour is at odds with that of regular magnetic materials. Beyond this fact, studies are also motivated by the prospect of using magnetic nanometer-sized objects for information storage.
We have synthesized Au nanoparticles which a ferromagnetic-like behaviour from 4K up to 400K.
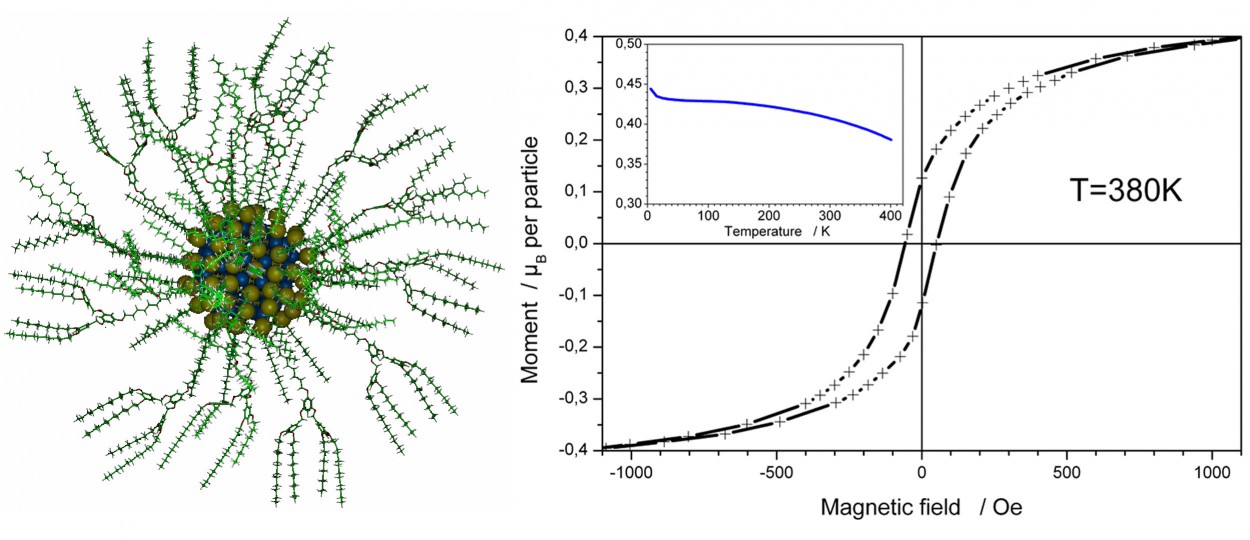
Amongst other reasons, the fact that the magnetization does not depend on temperature (inset with blue curve) has let us speculating about possible mechanisms which could lead to the observation of such unusual magnetic behaviour. As of today, we tentatively suggest that so-called “persistent currents” flow in the nanoparticles.
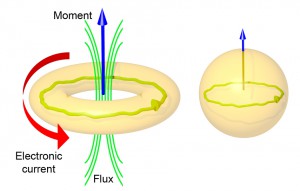
In mesoscopic metal rings that are smaller than the electron’s phase coherence length, currents can flow “forever”, even if the metal is not in a superconducting state, under the condition that the ring circles around a magnetic flux. To observe these currents, the temperature has to be sufficiently low to reduce the probability of inelastic scattering from phonons and other electrons, and the ring circumference must be sufficiently short such that phase coherence of the electrons is preserved around the ring. Such persistent currents are therefore usually observed in rings with a diameter smaller than 1 µm and at temperatures lower than 1 K.
Persistent currents exist in rings that have a finite resistance and can only be revealed by the small magnetic moment that they generate since inserting a current-measuring device inthe ring would kill the phase coherence of the electrons. A variability of the response from sample to sample is theoretically expected, and experimentally observed persistent currents have been found to vary strongly from sample to sample. The magnetic moment of the ring can have the same direction as the applied magnetic field (paramagnetic response), or the opposite (diamagnetic response), depending on whether the number of conduction electrons is even or odd. Statistically, in an ensemble of independent rings, these fluctuations average out. However, the ensemble-averaged current is slightly paramagnetic. This shift of the average towards positive and possibly large values results from the fact that each ring has a constant number of electrons and the problem must therefore be described with the canonical ensemble. Dissipation-less current flow in a resistive circuit looks counterintuitive but is indeed possible if this peculiar state is the ground state of the system. This is conceptually equivalent to electrons orbiting around atoms without losing energy by synchrotron radiation and generating permanent orbital magnetic moments, even in the ground state. As mentioned previously, the circuit needs not have zero resistance and furthermore, weak dissipation or noise does not result in the disappearance of the persistent currents. In any case, such currents have been observed experimentally by several groups in rings made of Cu, Au, Al or semiconductors.
Our proposal is that the magnetic properties of Au and possibly other metal nanoparticles are the result of persistent currents. These currents would be induced by the magnetic field which is applied in most magnetic measurements, in particular SQUID magnetometry, or even stray fields such as those from the magnetic stirrer used during the synthesis. Interestingly, the theory of persistent currents can directly be transposed to nanoparticles, without the need to develop a specific model.
The temperature at which persistent currents disappear (Thouless temperature) scales as 1/r2, implying that nanoparticles having a diameter up to ~20nm should support persistent currents above room temperature. Magnetic moments of tens of µB per particle are possible. Last, it has been predicted that persistent currents could become self-sustained, that is flow even in the absence of an external magnetic field, therefore explaining the occasional ferromagnetism of gold nanoparticles. Local dipolar interactions between nanoparticles could also play a role, especially when the nanoparticles are ordered in a lattice (mesophase).
Persistent current probably develop only in a minority of nanoparticles, for reasons which remain today unclear. The cristallinity of the particles or their shell structure might play a role.
Magneto-optical control of a Mn12 nanomagnet
J.L. Gallani & B.Donnio
Single Molecule Magnets (SMM) are paramagnetic molecules with a non-zero and usually large individual spin S. Under appropriate field and temperature conditions a stable magnetization in the +S or −S state can be retained for long periods of time (years), the two spin states being separated by an energy barrier. The effect is purely intra-molecular and such molecules therefore literally behave as nano-magnets, hence their name. There is a considerable research activity around these systems, mostly for the development of high-density magnetic storage of information or the implementation of quantum algorithms for computation with SMM-based qubits. For both applications the control of the magnetic state is paramount. So far, attempts at probing the spin state have been performed on isolated molecules using a STM, or on larger assemblies using microwave irradiation in ESR cavities or with SQUID devices. We have discovered that irradiation at optical wavelengths can trigger at will an increase or a decrease of the magnetic moment of a SMM, even though the energy of the photons does not correspond to a precise electronic or spin transition. Using the proper light and field sequence, the magnetization of the system can be driven between at least three different stable states. The consequences of these observations are manifold: they bring a means of controlling molecular magnets, open prospects in the field of quantum computing, and may enable the realization of coherent microwave sources through stimulated superradiance.
The potential energy of a SMM is usually pictured as a double well with (2S+1) energy sublevels which, in a first approximation, can be labelled by integer quantum numbers +S > mS >-S. Naturally, there also exist many molecular energy levels located at higher energies. After a SMM has been magnetized at low temperature by an external field, one generally considers that its magnetization can relax down to equilibrium either via a thermally activated process over the energy barrier or by spin tunneling through the barrier. Combinations of the two processes, i.e. phonon assisted tunneling, are also possible.
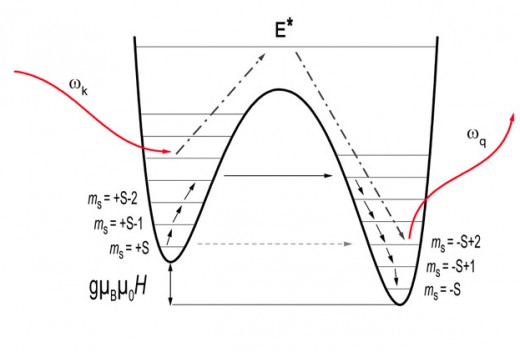
The relaxation to equilibrium (i.e. M = 0) is not the only relaxation process. In fact the whole magnetic behavior of SMM should rather be seen as something dynamic, under the influence of several time-dependant processes. In particular, the response of a SMM to an applied field also is time-dependant, as exemplified by the fact that the shape of hysteresis curves varies with the field sweep rate: it takes some time for the molecules to go from the metastable to the stable well, and the magnetization therefore always lags behind the applied field. Similarly, when a static magnetic field is applied, the metastable well drains out and the stable one is slowly populated. The rate at which quantum tunneling of the magnetization occurs is set by several factors: temperature, applied external field, angle between applied field and molecule easy axis, dipolar field from adjacent molecules and nuclear spins.
Because of these relaxation processes, the magnetization M of a SMM to a time-varying magnetic field H is hysteretic. The animation below illustrate this point : in the M/H plane, the magnetic state of the SMM is bound to this hysteresis curve (blue curve).
Now, if at any position on this hysteresis a light pulse is sent on the SMM, its magnetization jumps onto what we call “the limit curve” (in red). The animation below first shows an upwards jump of M from the lower branch of the hysteresis curve, then a downwards jump from the upper branch (i.e. a demagnetization). These two cases demonstrate that the proper combination of light and magnetic field can drive the system between different stable magnetic states. These results seem to be quite general as similar observations have been made on various SMM.